The turtle migrated to the computer screen where it lives as a
graphics object. Viewing the screen is like looking down on the
mechanical turtle from above.
The screen turtle also understands forward and right.
 |
 |
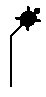 |
|
forward 50
|
right 45
|
forward 25
|
Following some exploratory messing around, a common first
Turtle activity is to draw a geometric shape. How about a
square?
 |
 |
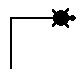 |
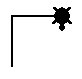 |
|
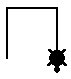
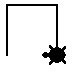
forward 50
|
right 90
|
forward 50
|
right 90
|
 |
 |
 |
 |
|
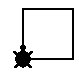
forward 50
|
right 90
|
forward 50
|
right 90
|
There's also a repeat command so that
repeat 4 [forward 50 right 90]
also draws a square.
How about a triangle?
repeat 3 [forward 50 right 60]
Oops! That's fine. Debugging is part of working in Logo.
Another important aspect of Logo is defining new procedures. We
drew a square using the instruction
repeat 4 [forward 50 right 90]
But if we tell Logo
square
Logo responds with the message:
I don't know how to square
So we teach Logo a new word.
to square
repeat 4 [forward 50 right 90]
end
Now if we type square, Logo draws a square just as if
we had typed repeat 4 [forward 50 right 90]. Logo has
learned a new word.
 |
 |
|
forward 50
|
square
|
Now that square is in Logo's vocabulary, the new word may be
used as part of another instruction. For example
 |
We can give this a name also.
to flower
repeat 36 [right 10 square]
end
|
|
repeat 36 [right 10 square]
|
In Logo, programming is done by adding new words to the
existing vocabulary. It's like learning a spoken language. New
words are defined using words you already know.
Things can get more complex. Procedures can take "inputs" so
that the information they use varies. We could write a square
procedure like this:
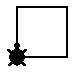
to square :size
repeat 4 [forward :size right 90]
end
Instead of always having a square of 50 units on a side we can
tell it how big to be:
 |
 |
 |
|
square 50
|
square 30
|
square 100
|
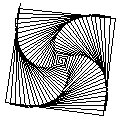
There's more:
to spiral :size :angle
if :size > 100 [stop]
forward :size
right :angle
spiral :size + 2 :angle
end
 |
 |
|
spiral 0 90
|
spiral 0 91
|
The traditional Euclidean geometry is built on abstractions: a
point that has no size; a line that has length but no thickness.
This is difficult for young learners to grasp. The turtle is a
real concrete object that may be seen and manipulated. Analytic
geometry rests on an outside frame of reference -- the
coordinate system. In contrast, turtle geometry is "body
syntonic". The turtle moves around as you do. You can identify
with it and understand what it is doing.
Turtle geometry was not intended to be a replacement for
traditional geometry but rather, as an alternative entry point
into geometry and mathematics in general. It is appropriate for
young children as well as adults.
The rationale behind turtle geometry is thoroughly explained by
Seymour Papert in Mindstorms
. Many versions of Logo come with tutorials and guide books
about turtle geometry.
While it is easy to get started with turtle geometry, it can
also get quite complex. The bookTurtle
Geometry, by Hal Abelson and Adrea diSessa includes
many advanced explorations with the turtle.
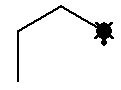
 It can be directed by typing commands at the
computer. The command forward 100 causes the turtle to
move forward in a straight line 100 "turtle steps". Right 45
rotates the turtle 45 degrees clockwise while leaving it in the
same place on the floor. Then forward 50 causes it to go
forward 50 steps in the new direction.
It can be directed by typing commands at the
computer. The command forward 100 causes the turtle to
move forward in a straight line 100 "turtle steps". Right 45
rotates the turtle 45 degrees clockwise while leaving it in the
same place on the floor. Then forward 50 causes it to go
forward 50 steps in the new direction.